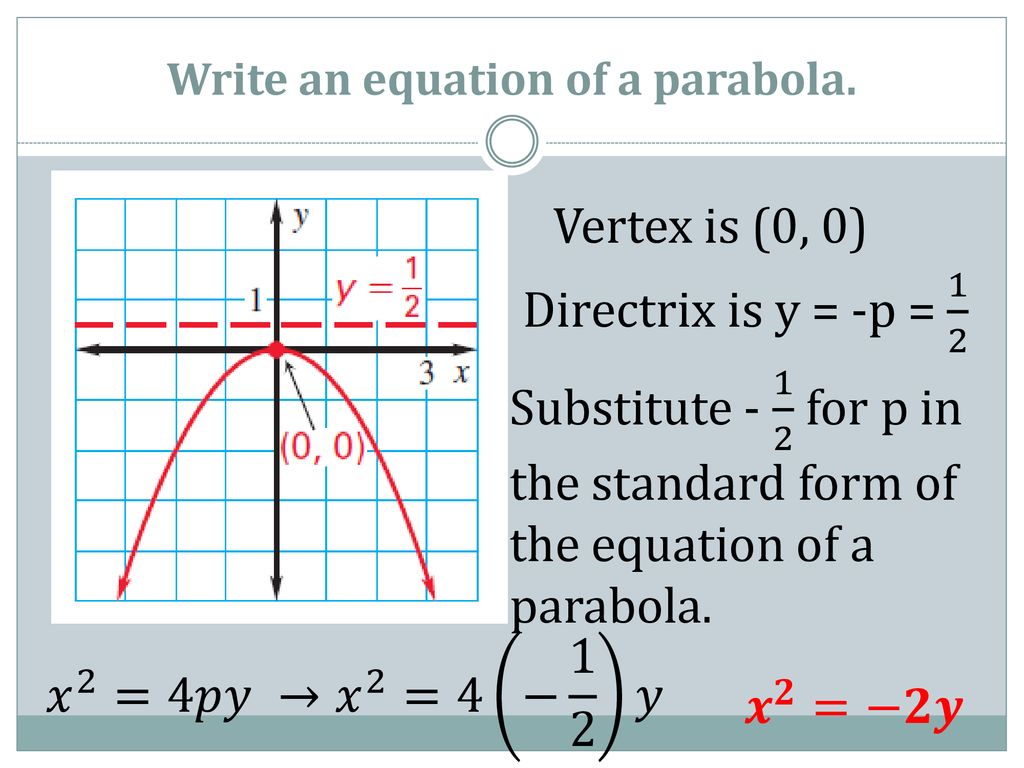
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Por um escritor misterioso
Last updated 21 fevereiro 2025

Day 18 Warm-Up 1) Which of the following problems is a circle and which is a parabola? Why? A) ppt download

Pre-Calculus Prep: Conic Sections - Graph the Ellipse

geometry - Focus of parabola with two tangents - Mathematics Stack Exchange

Conic sections: Analyzing Conic Sections with the Algebraic Method - FasterCapital
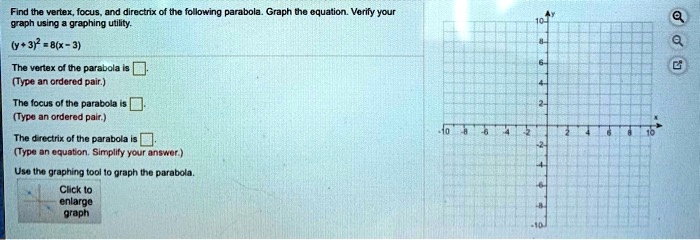
SOLVED: Find the vertex, focus, and directrix of the following parabola. Graph the equation using a graphing tool. (y + 3)^2 = 8(x - 2) The vertex of the parabola is (2,
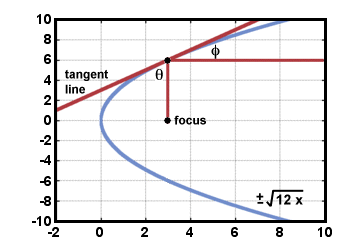
Conic Sections Parabolas Summary & Analysis

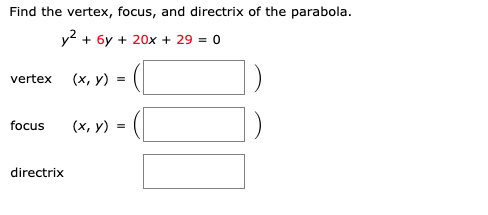
Solved Find the vertex, focus, and directrix of the
Solved Match the equation with one of the conics. x2 + x2 =

SOLVED: Use the given equation to identify the direction the parabola is opening, and the vertex, focus, and directrix for the parabola. Then, graph the parabola. Include the focus, vertex, directrix, and
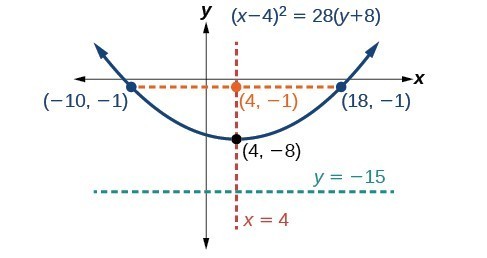
Graphing Parabolas with Vertices Not at the Origin, College Algebra

Find a polar equation of the conic with its focus at the pole. Parabola; (8, 0)

Conic sections: Analyzing Conic Sections with the Algebraic Method - FasterCapital
How to draw a dot plot - Quora

Find the major axis, minor axis, foci and graph an ellipse

Parabola CE with ANSWERS - H. Algebra 2 Name D u2m0F1c6z AKNuetxap jSuoCfvtywNanrWeW pLBLPCp.V U aAAlPlT r ihgfhXtHsY LrZeqs eXryvweXdi. Parabola
Recomendado para você
-
 DirectX Control Panel - Download21 fevereiro 2025
DirectX Control Panel - Download21 fevereiro 2025 -
 DirectX 12 chegou finalmente ao Windows 7 graças ao World of Warcraft21 fevereiro 2025
DirectX 12 chegou finalmente ao Windows 7 graças ao World of Warcraft21 fevereiro 2025 -
Directx 9.0C Compatible 3D Accelerated 64Mb Video Card Download - Colaboratory21 fevereiro 2025
-
 How to Check What Version of DirectX Is Installed - MajorGeeks21 fevereiro 2025
How to Check What Version of DirectX Is Installed - MajorGeeks21 fevereiro 2025 -
 TiledLighting11 DirectX® 11 SDK Sample - AMD GPUOpen21 fevereiro 2025
TiledLighting11 DirectX® 11 SDK Sample - AMD GPUOpen21 fevereiro 2025 -
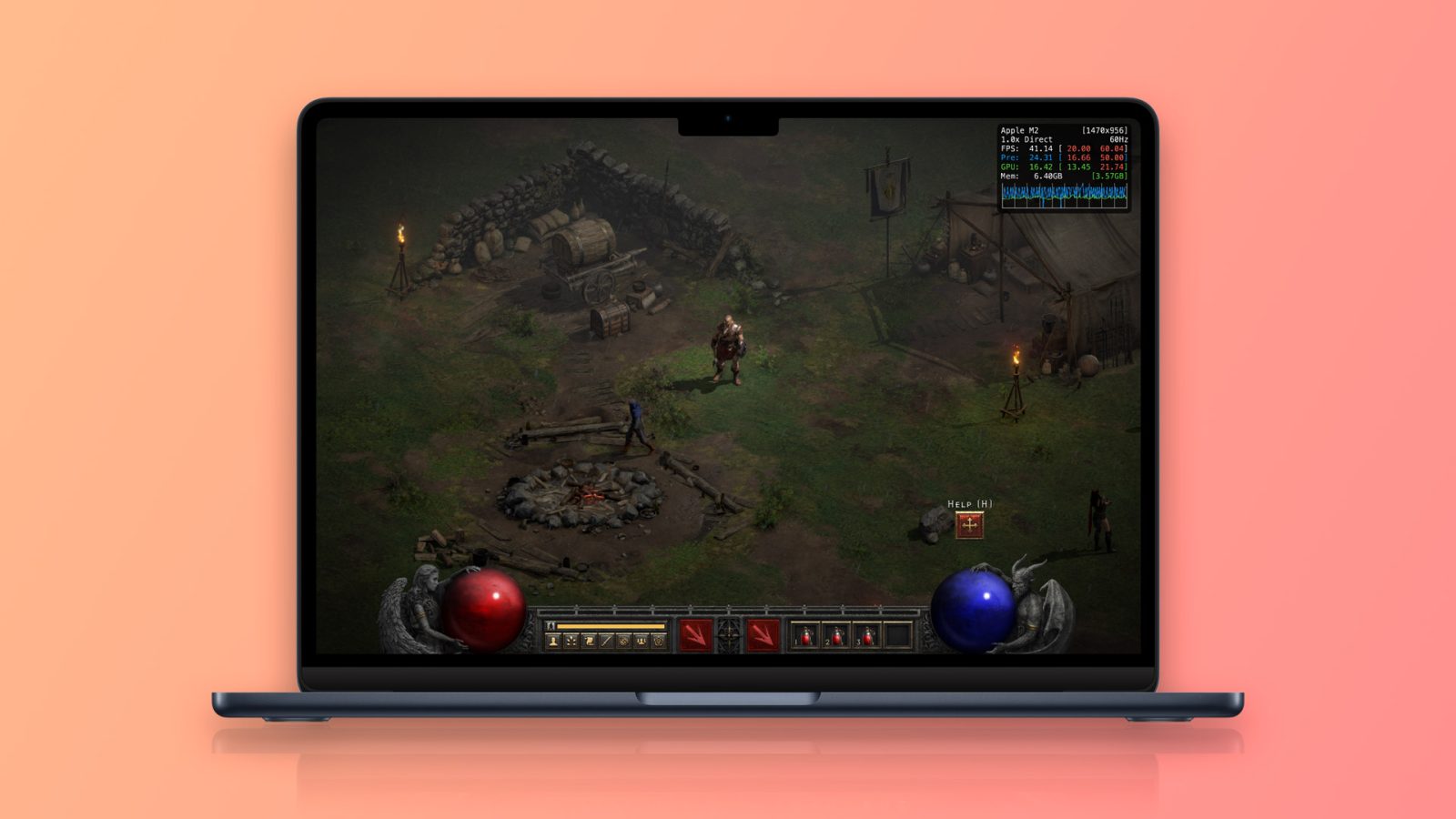 CrossOver announces DirectX 12 support coming to macOS21 fevereiro 2025
CrossOver announces DirectX 12 support coming to macOS21 fevereiro 2025 -
 The Witcher 3 Next Gen - DirectX 11 vs DirectX 12 - Benchmark Comparison21 fevereiro 2025
The Witcher 3 Next Gen - DirectX 11 vs DirectX 12 - Benchmark Comparison21 fevereiro 2025 -
 NVIDIA Ion Reference PC Platform Deep Dive21 fevereiro 2025
NVIDIA Ion Reference PC Platform Deep Dive21 fevereiro 2025 -
 MegaRace: MR3 • PC – Mikes Game Shop21 fevereiro 2025
MegaRace: MR3 • PC – Mikes Game Shop21 fevereiro 2025 -
Solved: Direct X 11.0 available; feature level 12.0 requi - Adobe Community - 1381405121 fevereiro 2025
você pode gostar
-
 Secret Invasion Episode 1 Resurrection Podcast21 fevereiro 2025
Secret Invasion Episode 1 Resurrection Podcast21 fevereiro 2025 -
 Alice Madness Returns Chapter 3 Memory Locations walkthrough21 fevereiro 2025
Alice Madness Returns Chapter 3 Memory Locations walkthrough21 fevereiro 2025 -
 Manga 94 Dragon Ball Super completo en español21 fevereiro 2025
Manga 94 Dragon Ball Super completo en español21 fevereiro 2025 -
 BONECO ROBLOX Club Roblox - Sunny 2211 - Ri Happy21 fevereiro 2025
BONECO ROBLOX Club Roblox - Sunny 2211 - Ri Happy21 fevereiro 2025 -
 NEW MAPPA ANIME! BUCCHIGIRI PV MAIN TRAILER REACTION21 fevereiro 2025
NEW MAPPA ANIME! BUCCHIGIRI PV MAIN TRAILER REACTION21 fevereiro 2025 -
 Elfen Lied (manga) - Anime News Network21 fevereiro 2025
Elfen Lied (manga) - Anime News Network21 fevereiro 2025 -
 RESPOSTAS ENGRAÇADAS de WHITELIST para GTA RP21 fevereiro 2025
RESPOSTAS ENGRAÇADAS de WHITELIST para GTA RP21 fevereiro 2025 -
 What's better than light in Blox fruits?21 fevereiro 2025
What's better than light in Blox fruits?21 fevereiro 2025 -
 5 CARROS RAROS e VEICULOS ESCONDIDOS EM GTA SAN ANDREAS21 fevereiro 2025
5 CARROS RAROS e VEICULOS ESCONDIDOS EM GTA SAN ANDREAS21 fevereiro 2025 -
 Life Lessons with Uramichi Oniisan, Dublapédia21 fevereiro 2025
Life Lessons with Uramichi Oniisan, Dublapédia21 fevereiro 2025