Casasteepest descent method

Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings

Por um escritor misterioso
Last updated 30 janeiro 2025
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
The Steepest-Descent Method - ppt video online download
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
Lecture 6: Slope and Free Energy (Chapter 6) - Lectures on Random Lozenge Tilings
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
Doubly periodic lozenge tilings of a hexagon and matrix valued orthogonal polynomials - Charlier - 2021 - Studies in Applied Mathematics - Wiley Online Library
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
Lecture 4: Counting Tilings on a Large Torus (Chapter 4) - Lectures on Random Lozenge Tilings
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
Lecture 8: Proof of the Variational Principle (Chapter 8) - Lectures on Random Lozenge Tilings
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
Skew Howe duality and limit shapes of Young diagrams - Nazarov - Journal of the London Mathematical Society - Wiley Online Library
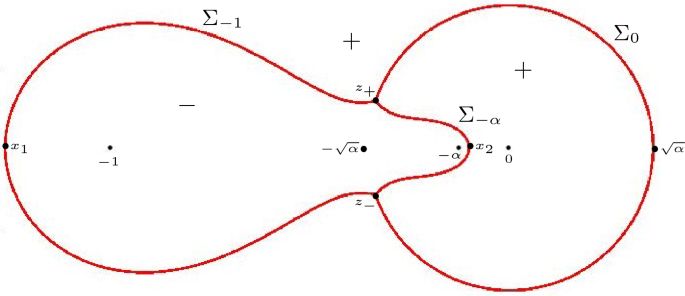
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
A Periodic Hexagon Tiling Model and Non-Hermitian Orthogonal Polynomials
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
The Steepest-Descent Method - ppt video online download
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
Lectures random lozenge tilings, Discrete mathematics, information theory and coding
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
Skew Howe duality and limit shapes of Young diagrams - Nazarov - Journal of the London Mathematical Society - Wiley Online Library
Recomendado para você
você pode gostar

© 2014-2025 phtarkwa.com. All rights reserved.