Rooks Problem -- from Wolfram MathWorld
Por um escritor misterioso
Last updated 19 janeiro 2025

The rook is a chess piece that may move any number of spaces either horizontally or vertically per move. The maximum number of nonattacking rooks that may be placed on an n×n chessboard is n. This arrangement is achieved by placing the rooks along the diagonal (Madachy 1979). The total number of ways of placing n nonattacking rooks on an n×n board is n! (Madachy 1979, p. 47). In general, the polynomial R_(mn)(x)=sum_(k)r_k^((m,n))x^k whose coefficients r_k^((m,n)) give the

Rooks Problem -- from Wolfram MathWorld

Rook polynomial - Wikipedia

Using Boolean Computation to Solve Some Problems from Ramsey Theory « The Mathematica Journal

Rook Polynomials: A Straight-Forward Problem – Feature Column

4_The Putnam Mathematica Competition (2001-2008).AMS by Fredi Luarasi - Issuu
IGraph/M Documentation
How many ways are there to place two identical rooks on a standard 8x8 checkerboard so that they are attacking each other? - Quora
Mathematica on the cheap [ David Antler ]

Posts Tagged with 'Advanced Math'—Wolfram
Recomendado para você
-
 How to Use Your Rooks effectively? - Remote Chess Academy19 janeiro 2025
How to Use Your Rooks effectively? - Remote Chess Academy19 janeiro 2025 -
 Rooks on Chessboard - Problems and Algorithms19 janeiro 2025
Rooks on Chessboard - Problems and Algorithms19 janeiro 2025 -
 discrete mathematics - n-rooks n-colors problem - Mathematics Stack Exchange19 janeiro 2025
discrete mathematics - n-rooks n-colors problem - Mathematics Stack Exchange19 janeiro 2025 -
 Problem - 1342E - Codeforces19 janeiro 2025
Problem - 1342E - Codeforces19 janeiro 2025 -
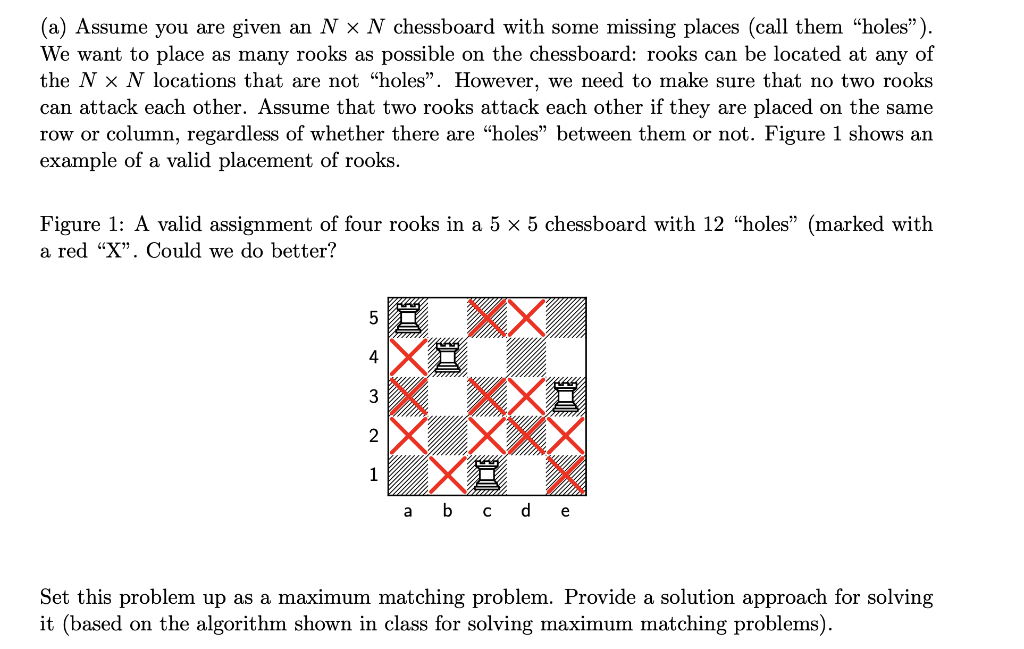 Solved (a) Assume you are given an N * N chessboard with19 janeiro 2025
Solved (a) Assume you are given an N * N chessboard with19 janeiro 2025 -
How many rooks can be placed on a chessboard so that no two rooks are attacking each other? - Quora19 janeiro 2025
-
Polinomios de Rook, PDF, Mathematics19 janeiro 2025
-
 Rook Polynomials: A Straight-Forward Problem – Feature Column19 janeiro 2025
Rook Polynomials: A Straight-Forward Problem – Feature Column19 janeiro 2025 -
 PDF) Construction of Rook Polynomials Using Generating Functions and mxn Arrays19 janeiro 2025
PDF) Construction of Rook Polynomials Using Generating Functions and mxn Arrays19 janeiro 2025 -
 Chess John D. Cook19 janeiro 2025
Chess John D. Cook19 janeiro 2025
você pode gostar
-
 Digerati - Jogos de Menina + de 800 Jogos : Digerati : Free Download, Borrow, and Streaming : Internet Archive19 janeiro 2025
Digerati - Jogos de Menina + de 800 Jogos : Digerati : Free Download, Borrow, and Streaming : Internet Archive19 janeiro 2025 -
 Friday Night Funkin' - Mommy Long Legs Sings Playtime (Vs Mommy19 janeiro 2025
Friday Night Funkin' - Mommy Long Legs Sings Playtime (Vs Mommy19 janeiro 2025 -
 Create a Creatures of Sonaria: All Creatures (March 2022) Tier19 janeiro 2025
Create a Creatures of Sonaria: All Creatures (March 2022) Tier19 janeiro 2025 -
 JEFusion Japanese Entertainment Blog - The Center of Tokusatsu: Death Battle - Wolverine VS Raiden19 janeiro 2025
JEFusion Japanese Entertainment Blog - The Center of Tokusatsu: Death Battle - Wolverine VS Raiden19 janeiro 2025 -
![Como jogar CS:GO: Tutorial completo [Atualizado – 2019]](https://i.pinimg.com/originals/c6/ce/6a/c6ce6a89b1771933fe1b5e29ce30c9cd.jpg) Como jogar CS:GO: Tutorial completo [Atualizado – 2019]19 janeiro 2025
Como jogar CS:GO: Tutorial completo [Atualizado – 2019]19 janeiro 2025 -
Tier list19 janeiro 2025
-
 Ikarus c42 hi-res stock photography and images - Alamy19 janeiro 2025
Ikarus c42 hi-res stock photography and images - Alamy19 janeiro 2025 -
 estilo de desenho animado de ilustração vetorial de motor motor 10424672 Vetor no Vecteezy19 janeiro 2025
estilo de desenho animado de ilustração vetorial de motor motor 10424672 Vetor no Vecteezy19 janeiro 2025 -
 História I still like your hair - História escrita por lemonworld - Spirit Fanfics e Histórias19 janeiro 2025
História I still like your hair - História escrita por lemonworld - Spirit Fanfics e Histórias19 janeiro 2025 -
 Practical Tips for the Tournament Player19 janeiro 2025
Practical Tips for the Tournament Player19 janeiro 2025

